Adaptive Horizon Actor-Critic for Policy Learning in Contact-Rich Differentiable Simulation

ICML 2024

Ignat Georgiev¹, Krishnan Srinivasan², Jie Xu³, Eric Heiden³, Animesh Garg^1,3

¹Georgia Tech ²Stanford University ³NVIDIA

Paper ArXiv Video Code

Adaptive Horizon Actor Critic (AHAC) is a First-Order Model-Based Reinforcement Learning algorithm that achieves 40% more asymptotic reward than Model-Free approaches across a set of locomotion tasks while being 1000x more sample efficient and more scalable to high-dimensional tasks.

Abstract

Model-Free Reinforcement Learning (MFRL), leveraging the policy gradient theorem, has demonstrated considerable success in continuous control tasks. However, these approaches are plagued by high gradient variance due to zeroth-order gradient estimation, resulting in suboptimal policies. Conversely, First-Order Model-Based Reinforcement Learning~(FO-MBRL) methods employing differentiable simulation provide gradients with reduced variance but are susceptible to bias in scenarios involving stiff dynamics, such as physical contact. This paper investigates the source of this bias and introduces Adaptive Horizon Actor-Critic (AHAC), an FO-MBRL algorithm that reduces gradient bias by adapting the model-based horizon to avoid stiff dynamics. Empirical findings reveal that AHAC outperforms MFRL baselines, attaining 40% more reward across a set of locomotion tasks and efficiently scaling to high-dimensional control environments with improved wall-clock-time efficiency.

Video

Adaptive Horizon Actor Critic

In our work we analyze the issues with first-order gradient estimation in differentiable simulation. We establish the under finite samples, these types of gradients exhibit empirical bias, particularly under stiff dynamics which ocur during contact. To address that we develop a new model-based reinforcement learning algorithm, Adaptive Horizon Actor-Critic (AHAC), which adaptively adjusts the horizon of the model-based optimization to avoid contact. This allows it to reduce bias and obtain asymptotically more optimal policies.

Results

Results from the Ant task show that AHAC outperforms all baselines in terms of asymptotic reward. Since we are mainly comparing against zeroth-order baselines, we normalize all rewards to the maximum achieved by PPO. Even though Ant is widely considered a solved task, we find that AHAC achieves 41% more reward than PPO, even if PPO is left to train for 3B timesteps.

Qualitatively, AHAC achieves more optimal and natural looking behaviour than our main baseline, PPO.

Aggregate asymptotic statistics across all tasks. The left figure shows 50% IQM with 95% CI of asymptotic episode rewards across 10 runs. We observe that AHAC is able to achieve 40% higher reward than our best MFRL baseline, PPO. The right figure shows score distributions which lets us understand the performance variability of each approach. Our proposed approach, AHAC, outperforms baselines even at the worst case, strengthening the case for first-order methods.

We also run experiments on classic tasks such as Hopper. Real robots such as Anymal. The popular Humanoid task with 21 degrees of freedom and an alternative muscle-actuated version with 152 degrees of freedom which we call SNU Humanoid. We find that AHAC maintains its asymptotic performance across the board. It also exhibits great sample efficiency, requiring 3 order of magnitude less data samples than PPO. Most impressively it also scales significantly better on high dimensional tasks. On the muscle-actuated humanoid, it achieves nearly twice the reward of PPO for the same training time.

Impressively, AHAC scales to a 152 action space muscle-actuated humanoid task, achieving 61% more reward of PPO.

Manipulation experiments

BibTeX

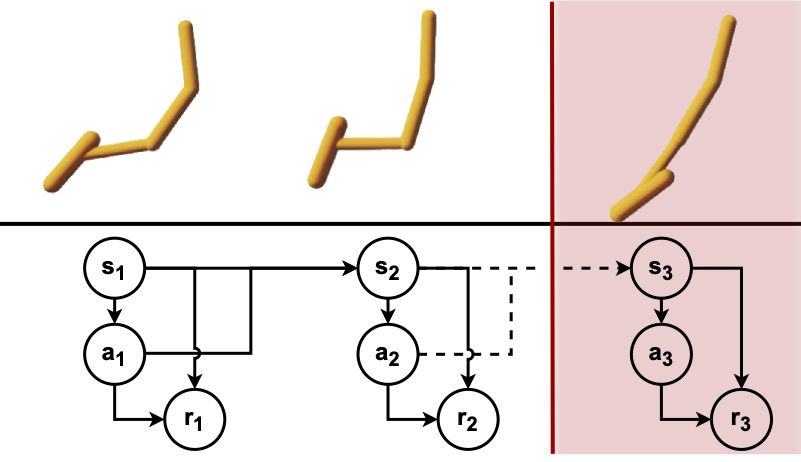
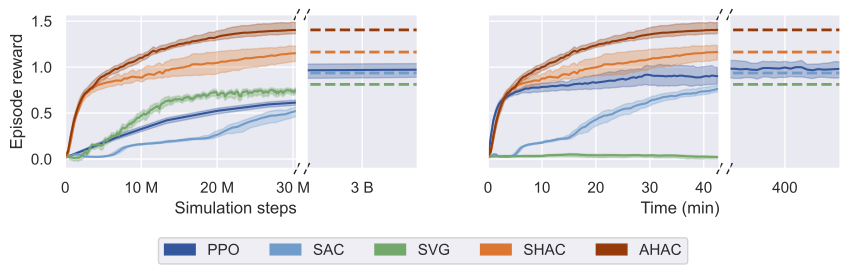
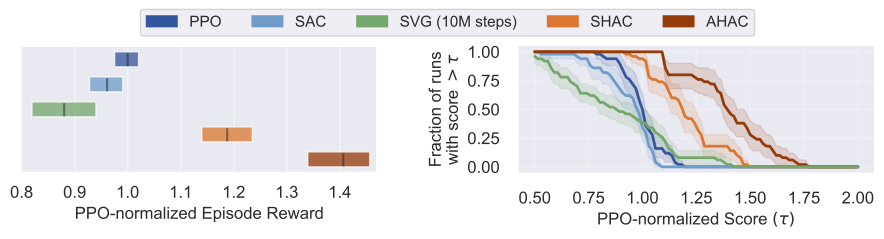
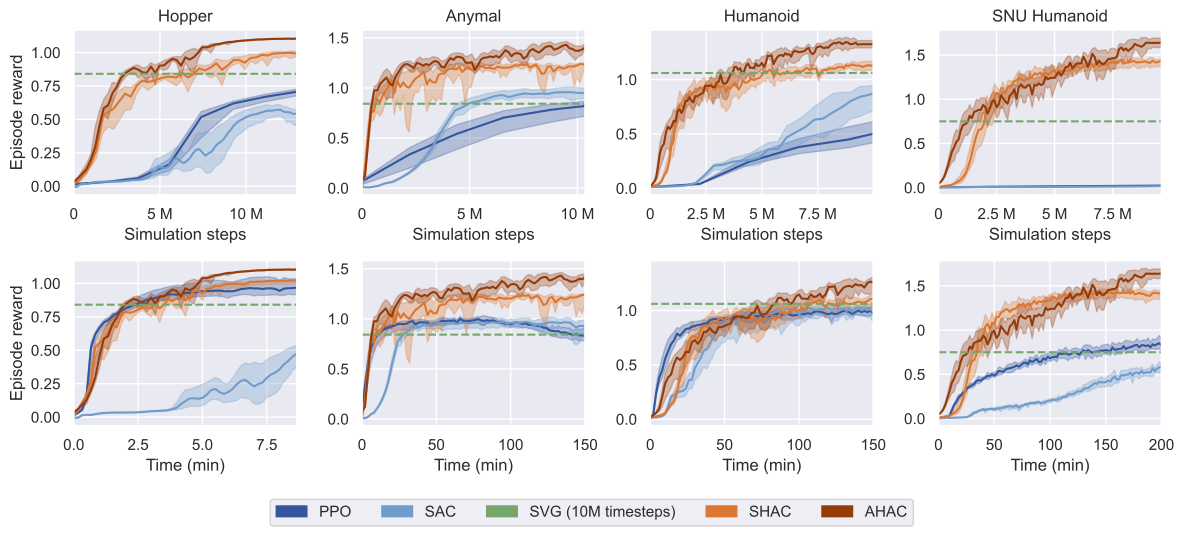
@inproceedings{georgiev2024adaptive,
  title={Adaptive Horizon Actor-Critic for Policy Learningin Contact-Rich Differentiable Simulation}, 
  author={Georgiev, Ignat and Srinivasan, Krishnan and Xu, Jie and Heiden, Eric and Garg, Animesh},
  booktitle={International Conference on Machine Learning},
  year={2024},
  organization={PMLR},
}